1. Incentives or yields in a protocol.
The rewards distributed through incentives when designing the tokenomics of your protocol are one of the most relevant aspects to attract liquidity to it.
Therefore, the main reason for distributing rewards in DeFi protocols is to reward those who contribute by providing liquidity when needed. Typically, we can see protocols where the rewards that are distributed are exaggeratedly high at the beginning and drop radically weeks later. We can also see other practices, such as manually adjusting rewards when profitability drops; but this technique - widely used in the crypto industry - is not very appropriate when the procedure can be optimized, modeled and programmed.
These poor or non-existent modeling of rewards or yields cause users to invest in a protocol for short periods of time only to disinvest a few hours, days or weeks later.
From Tutellus we did not want to attract these users or show to the community a behavior along these lines of incentivizing the short term and behave as many DeFi protocols have done, which attract a lot of capital with crazy yields to fall shockingly a few weeks later. When we design TUT tokenomics we seek to reward the earliest users and create with them a long-term relationship of trust that will last for years: you -token holder- contribute liquidity to my protocol, and I will reward you more and more for years to come.
2. Traditional reward distribution in DeFi protocols.
We can make an estimate of the return a protocol offers over time based on monthly rewards and assuming: that all tokens in the protocol go to rewards and that 100% of the market contributes to the protocol.
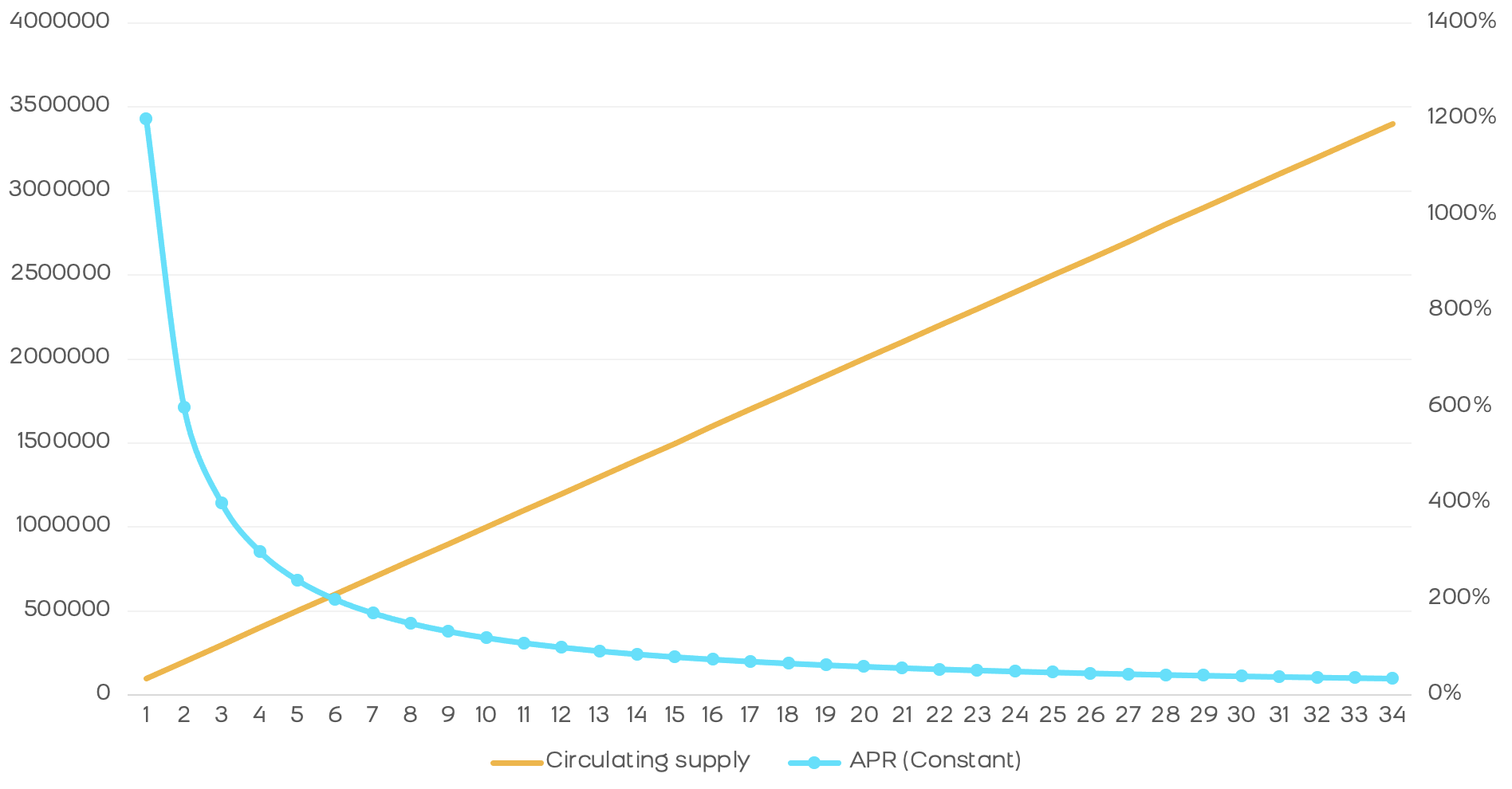
In this model we see the very sharp drop from 1200% APR to 100% in just 1 year. In addition, after 3 years we see that this APR drops to 30%. There is an abysmal difference that will only attract holders in the first weeks, behaving like "mercenaries" and looking for other more profitable protocols as soon as the APR starts to fall. This effect is what we have experienced in the vast majority of clones of the main AMMs and many blockchains, especially in the BSC.
3. Tutellian reward distribution.
To combat this effect and from Tutellus we have devised a formula to automatically adjust the distribution of rewards to the amount of tokens in circulation. This way we can reward users in a much more efficient way. Basically we use a first-degree function (a straight line) to define the distribution, whose fundamental characteristics are: An acceleration of the rewards (slope M) and a starting point (N).
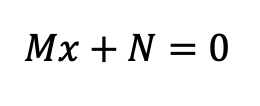
For the initial instant, with 0 tokens in the market, no rewards are distributed. Therefore, N = 0. According to our whitepaper, the amount of rewards distributed over the first 36 months is 64M, which means that the integral of the distribution line between 0 and 36 is equal to 64M.
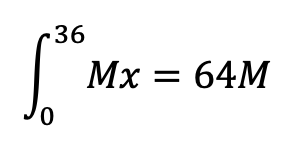
Thus, we can obtain the slope of the line by solving the integral, obtaining the following estimate:
4. Benefits of Tutellian reward distribution.
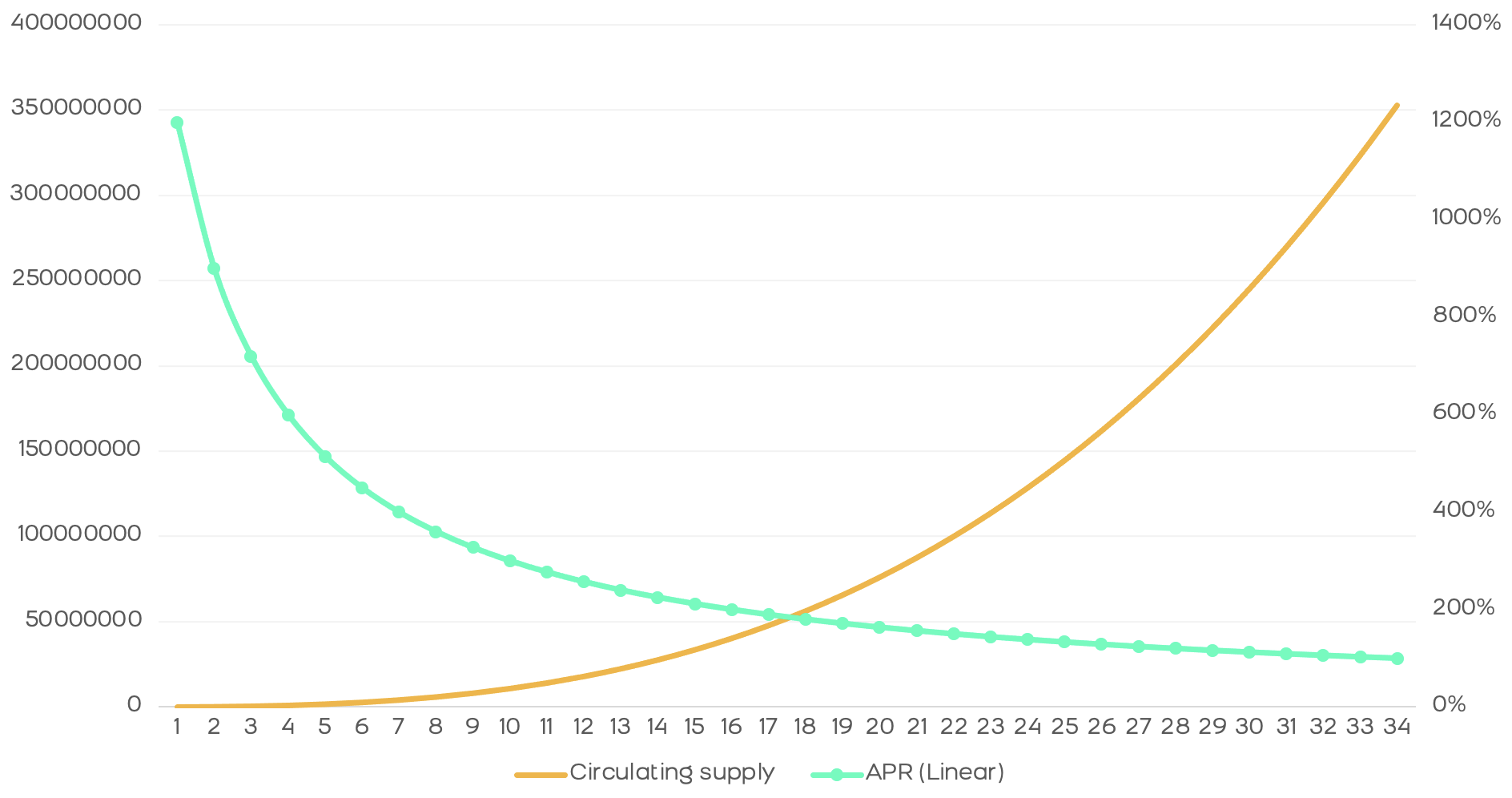
In short, we see that the drop in rewards is less abrupt and the annual return is higher than in a constant distribution, as we can see in the following comparison.
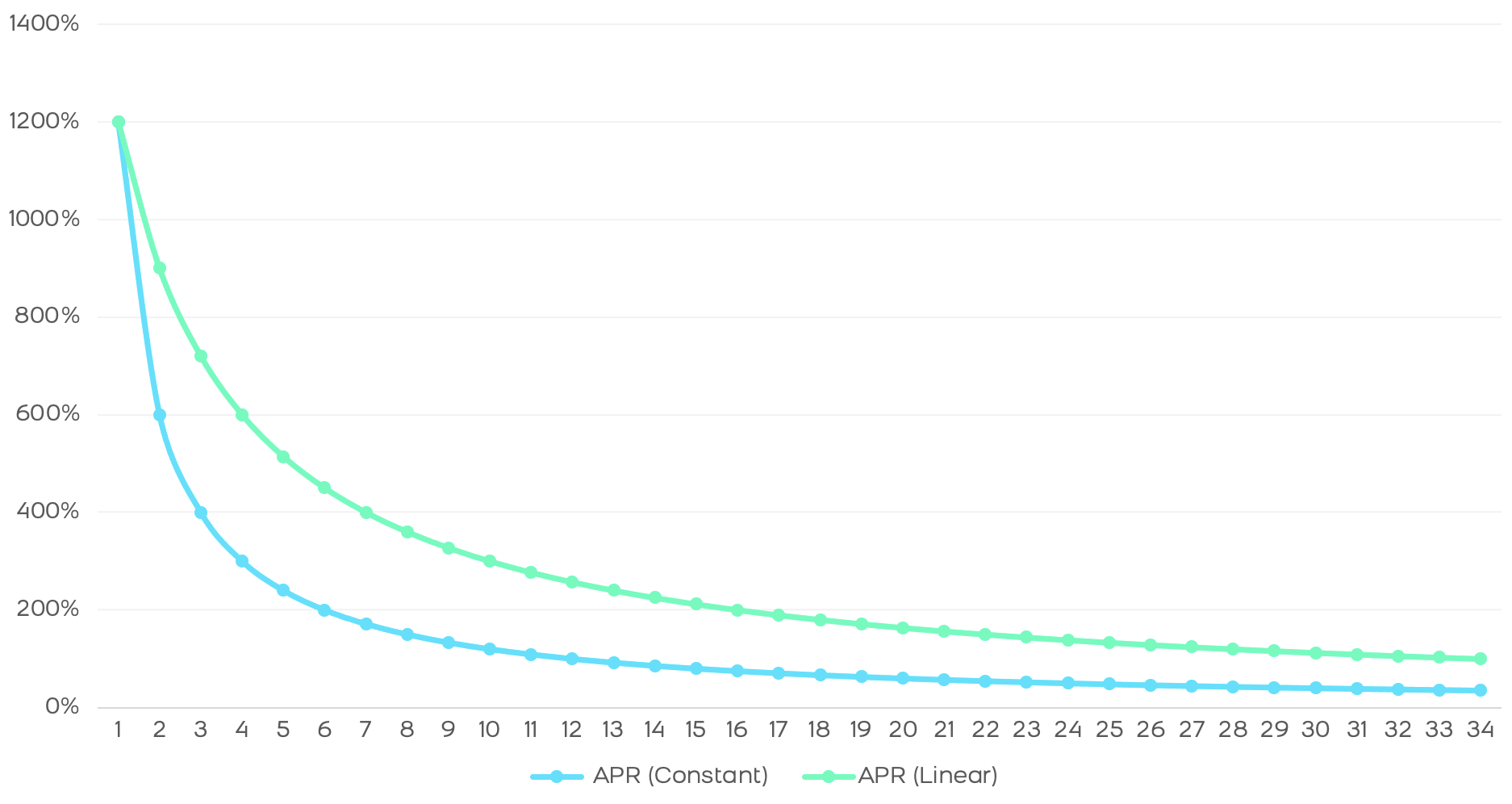
The distribution of tutellian rewards is more efficient and generates a higher return than constant rewards. Moreover, the amount of tokens in the market obeys an exponential function, this behavior being more natural since - normally - protocols do not follow a linear growth rate, but rather accelerate their growth over time and, therefore, it is optimal for rewards to adjust to this increasing rate.
Briefly, to better understand the behavior of this revolutionary distribution of rewards at the blockchain level already, you must understand that the release of tokens in a blockchain does not occur continuously but discretely, block by block, every few seconds. Therefore, we must translate this formula into discrete language.
Knowing the amount of tokens to be distributed and the initial and final block of the reward period we can clear the slope M, which is stored as a constant in the smart contract. Subsequently, the calculation of the rewards released between block A and block B is calculated by solving the integral we have seen in that range:
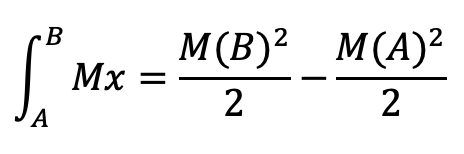
This last part is what is written in the contract: knowing the initial and final block, we can quickly and easily obtain the rewards released in that period.
5. Conclusions: let's encourage the long term.
From Tutellus and with the launch not only of the TUT, but of all the projects and tokens of our ecosystem, it is clear to us that we have to bet on rewarding holders who contribute liquidity continuously in the long term. We must design procedures that discourage short-termism and incentivize sustained and long-term contributions.
Thus, a reward distribution that accelerates rewards over time, like the effect of compound interest, encourages the liquidity provider to continue to contribute liquidity to your protocol.
At the same time, with the mathematical functions described above, we are able to maintain APRs above 100% during the entire incentive program (3 years), enough time for the protocol to have absorbed a lot of liquidity and the project to go on autopilot with the help of the community.
If you are creating your own tokenomics we invite you to use "tutellian mathematical modeling". Your token will thank you and your holders will be happier. And we will be happy to share this knowledge with the community :)
Finally, keep in mind that we still have more than 34 months of extraordinarily profitable yield farming ahead of us in Tutellus with the TUT. So you know, buy TUTs and farm. And if you don't know how to do it, in the FAQs section you have videos and posts where we talk both about how to buy TUTs and how to farm TUTs.
¡Let's continue!
Descubre más artículos en el Criptoblog sobre...




